LAWS OF
EXPONENTS

• Return

Scroll for more!

Product Rule

This rule is used to multiply expressions with the same bases. The rule can be used to simplify two expressions that have a multiplication operation between them in this case."To multiply two expressions with the same base, add the exponents while keeping the base the same."

1.) (m²²)(m⁹)(m⁷)Solution:Copy the same base, which is the variable m. Next, add the exponents. It should be:m²² ⁺ ⁹ ⁺ ⁷ = ?Once they are all added, the answer should be:m²² ⁺ ⁹ ⁺ ⁷ = ³⁸ or m³⁸2.) 2³ . 4²Solution:For this item, the bases must be multiplied. Once multiplied, the answer should be:8³ ⁺ ² = ?Next, add the exponents 3 and 2. It should now be:8³ ⁺ ² = ⁵ or 8⁵Always remember to simplify your answer to its lowest form. Once simplified, the answer must now be:8 . 8 . 8 . 8 . 8 = 32,768

Quotient Rule

Now for this rule instead of multiplying, we divide expressions with the same bases. Without actually using the division method, the only requirement is that the bases of the two expressions must match."To divide two expressions with the same base, subtract the exponents while keeping the base same."

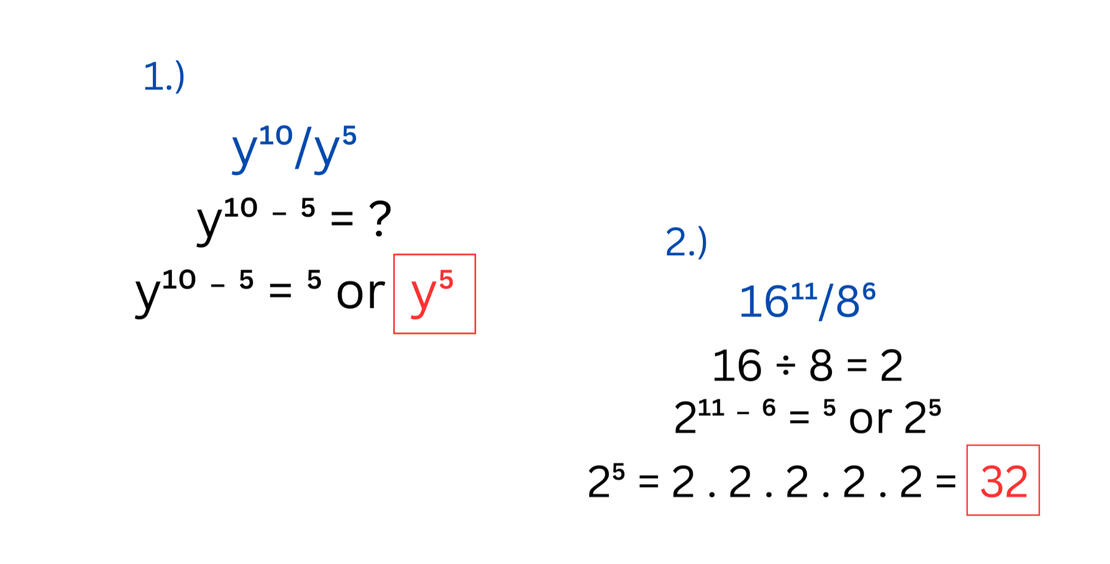
1.) y¹⁰/y⁵Solution:Just like the product rule, copy the same base when dividing. In this item, we have the variable y. After that, subtract the exponents 10 and 5. It should now be:y¹⁰ ⁻ ⁵ = ?Once the operation is performed, the answer must be:y¹⁰ ⁻ ⁵ = ⁵ or y⁵2.) 16¹¹/8⁶Solution:When dividing exponents of different bases, simply divide them both. The answer should then be:16 ÷ 8 = 2After dividing the bases, proceed with subtracting the exponents.2¹¹ ⁻ ⁶ = ⁵ or 2⁵Simplify the exponent until you get your final answer.2⁵ = 2 . 2 . 2 . 2 . 2 = 32

Power of a Power

The use of this law simplifies (aᵐ)ⁿ expressions. Simply multiply the exponent by the power to bring a number with an exponent to that power.For a single exponent, these can be easily multiplied.

1.) (7a²b³c⁴)⁵Solution:Distribute the exponent from the outside of the parenthesis to the exponents inside the parenthesis. In this process, the exponents must be multiplied. Afterwards, multiply some of the exponents to get the final power.7⁵a²⁽⁵⁾b³⁽⁵⁾c⁴⁽⁵⁾7⁵a¹⁰b¹⁵c²⁰Next, make sure to simplify the terms to get your final answer:16807a¹⁰b¹⁵c²⁰2.) (a¹⁰b¹²c¹⁴⁾⁵Solution:Distribute the exponent to the expression inside the parenthesis. For this process, you will get:a¹⁰⁽⁵⁾b¹²⁽⁵⁾c¹⁴⁽⁵⁾a⁵⁰b⁶⁰c⁷⁰Since there is no need for any base to be simplified, your final answer is going to be:a⁵⁰b⁶⁰c⁷⁰

Power of a Product

When a product is raised to an exponent, the result can be found using the Power of a Product Rule. You can distribute the exponent to each factor and multiply separately if the product of two real numbers that are not zero is raised to an exponent.

1.) (8ghi)³Solution:Distribute the exponent to the exponents inside the parenthesis. It shall now be:8g³h³i³Simplify the base and the exponent until you get your final answer. It shall now be:83 = 8 . 8 . 8
= 512512g³h³i³2.) (6jkl)²Solution:Distribute the exponent before multiplying the terms inside the parenthesis. It should now be:6²j²k²l²Make sure to simplify so you can get your final answer.6² = 6 . 6
= 36The final answer is:36j²k²l²

• More